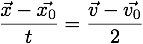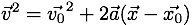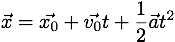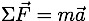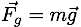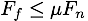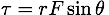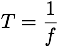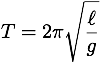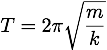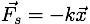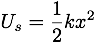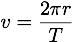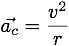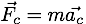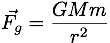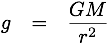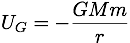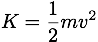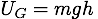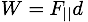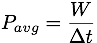The Physics Calculator (beta)

Training Wheels for Your Mind

The physics calculator (launch web app.) is a free tool for solving common introductory mechanics problems.^† It is optimized for smart phones and tablets but accessible to any computer with a web connection. Users choose a topic or topics to work with, and the calculator walks them through a step-by-step problem solving process. Essentially, it is a set of training wheels. The calculator makes each step of the process explicit, allowing students to internalize them and eventually set the calculator aside as they tackel more complicated problems. Similarly, the calculator can introduce quantitative problems to courses wishing to avoid standard mathematical formalism, such as conceptual physics or "poet's" classes.

Solving Kinematic Equations, a Use Case

How long does it take a car to go from zero to 27.0 m/s if it accelerates at a constant 10.8 m/s/s?

Choosing a relevant topic. (simulated image)

To help with the problem solving process, the calculator will ask you a number of questions.

What is relevant?

First, we choose a relevant topic or topics. Each topic is associated with a set of equations. By choosing a topic, and its associated equations, we define a set of possible routes for solving our problem. Here we're dealing with a constant acceleration. So we'll choose "kinematics."

What do you know?

The calculator presents us with a set of variables drawn from the topic(s) we just picked, and we place a check next to each variable we know. In this case, we know the car's acceleration as well as its initial and final velocities.

What are you looking for?

We want to know how long it takes the car to "go from zero to 27.0 m/s." So we tell the calculator that we want to solve for time. Now that it knows what we know and what we want to know, it can help us decide which equation to use.

Data Entry

How do you want to get there?

We are presented with a set of equations, drawn from our earlier selection. We can click on those equations that contain the variable we are looking for and only variables that we know. If we see an equation that we could use if we knew one more variable, we could consider solving for that variable, adding it to our know values and solving for the variable we wanted in the first place. This is something the calculator can help us out with, but for this problem, it's not a concern. It turns out that there is one equation that will work for us (i.e., 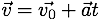). So we click/tap it.

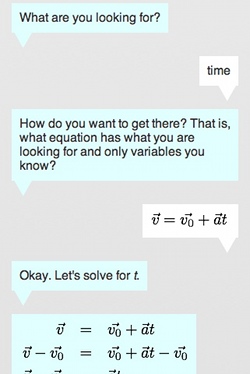
Reviewing your work.

Data Entry

The calculator takes our equation and solves for the variable we want to know (e.g. t). We enter values for those variables we know (i.e. a, v₀, and v), and we hit the "Solve" button.

Check Your Work: Is this your answer?

The calculator plugs our values into the equation we choose and produces an "answer" (2.5 s), but before we call it The Answer, we should check our work. Always ask yourself, "does this answer make sense?" Compare it to something you know well. For example, if you are calculating the speed of a baseball, it should raise a red flag if it's moving faster than the speed of sound. In this example, if you know something about cars, is our answer in the realm of possibility?

Supported Topics and Associated Equations^†

Kinematics